Best Methods to Convert Binary to Hex Instantly

Need to convert binary to hex? Binary numbers are made of 0s and 1s and can be long and difficult to manage. By converting them to hex, which uses 0-9 and A-F, you make them more readable and compact. This article will show you simple methods to convert binary to hex.

Key Takeaways

Understanding the binary and hexadecimal systems is essential for simplifying the representation of large binary values, with each hexadecimal digit representing four binary digits.

Binary to hexadecimal conversion can be performed directly by grouping binary digits or indirectly via decimal conversion, each method having its own benefits and applications.

Online tools like PagesTools.com offer efficient, user-friendly, and error-free binary to hexadecimal conversion, demonstrating the practical benefits of digital aids in managing complex processes.

Introduction

Ever wondered how the massive streams of binary digits that pulse through the veins of our computers and digital devices are translated into a form that is more compact and readily understandable by humans? This transformation is the essence of binary to hexadecimal conversion, a process that packs lengthy binary strings into a neat hexadecimal format. Whether you’re a programmer, an engineer, or just a curious learner, mastering the art of converting binary to hexadecimal is a key skill in the digital era. From utilizing direct and indirect methods to leveraging tools like PagesTools.com, this post will provide you with the knowledge to confidently convert binary strings into their hexadecimal counterparts and understand the underlying principles at play.

Understanding Binary and Hexadecimal Systems

At the core of digital communication, data storage, and processing lies the binary system – a language consisting solely of zeros and ones. Yet, representing large binary values can be cumbersome and prone to errors. This is where the hexadecimal system comes into the picture, providing a more compact and error-resistant format. By mapping every four binary digits to one hexadecimal digit, we achieve a cleaner, more readable representation of data.

For those venturing into computing and digital electronics for programming, data analysis, or troubleshooting, it’s essential to comprehend the relationship between these two systems.

What is a Binary Number System?

Binary, the fundamental language of all computing systems, operates on a base-2 numeral system. This system uses only two symbols: ‘0’ and ‘1’, each representing a power of two. Every digital device, from the smartphone in your pocket to the supercomputer crunching complex datasets, speaks this language internally. The binary system’s simplicity allows for straightforward circuitry design, yet it poses a challenge in readability and manageability when dealing with large numbers.

Hence, the binary to hexadecimal conversion becomes a bridge, enabling humans to interact with binary data in a more comprehensible form.

Binary To HEx by PagesTools.com

Navigating the digital landscape requires not just understanding, but also the right tools for the job. When it comes to binary to hexadecimal conversion, PagesTools.com offers a sleek, efficient tool that takes the tediousness out of the process. With the capacity to handle direct input or even file uploads containing binary data, this online converter streamlines the task, allowing you to focus on what really matters - the result.

This tool exemplifies how digital solutions can simplify intricate processes. It’s readily available and capable of converting binary digits into hexadecimal form swiftly.

What is a Hexadecimal Number System?

The hexadecimal system, a base-16 powerhouse, extends beyond the binary system’s two symbols by incorporating the entire numeral set from 0 to 9 and six additional symbols from the English alphabet: A to F. This system is not just a preference but a necessity in computer science, offering a concise way to represent binary data. With one hexadecimal digit encapsulating four binary digits, you can represent a byte (eight binary digits) with just two hexadecimal characters.

Programmers routinely use hexadecimal as a lingua franca for binary numbers, finding it invaluable in making sense of the complex data structures that underpin modern computing.

Direct Method: Binary to Hex Conversion Using Grouping

When it comes to converting binary to hexadecimal, the direct method is a straightforward approach that involves grouping binary digits. This process reduces complexity by bundling each set of four binary digits into a single hexadecimal digit. By applying this method, you sidestep the cumbersome binary strings and quickly arrive at a hexadecimal number that’s far easier to read and understand.

We’ll examine this method in detail, breaking it down into three steps: grouping binary digits, identifying corresponding hexadecimal values, and integrating them to reveal the final result.

Grouping Binary Digits

The journey from binary to hexadecimal, also known as hex binary, begins with grouping. Picture your binary number as a train of digits rolling in from the right; your task is to organize these digital passengers into quartets. Starting from the rightmost digit, you form groups of four, adding leading zeros if necessary to complete each compartment.

These four-digit groups are the building blocks of your hexadecimal number, each one poised to transform into a hex digit that carries the same value but in a more compact and readable form.

Finding Corresponding Hexadecimal Digits

Once your binary digits are neatly grouped, it’s time to find their corresponding hexadecimal number. Each binary quartet corresponds to a single hexadecimal digit, and this is where a conversion table becomes your best friend. With just a quick reference, you can match each group to its binary hexadecimal equivalent, from the simplest 0000 to 1111, translating to 0 through F respectively.

This step is like decoding a secret message where each group reveals a character, leading you one step closer to your final hexadecimal masterpiece.

Combining Hexadecimal Digits

With each group of binary digits now paired with its hexadecimal equivalent, the final step is to weave these digits into a single string. Start from the leftmost group and work your way to the right, concatenating each hexadecimal digit to form the complete number.

This final hexadecimal number is a condensed version of the original binary string, offering the same value in a fraction of the space. It’s a satisfying conclusion to a process that showcases the elegance of mathematical translation.

Indirect Method: Binary to Hex Conversion via Decimal

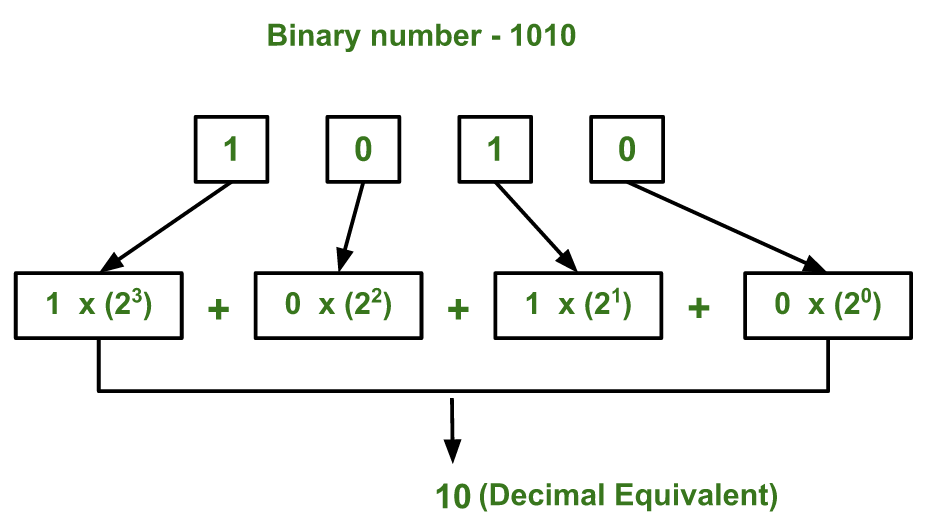
While the direct method offers a quick path from binary to hexadecimal, the indirect method introduces an intermediary step: converting to decimal first. This two-stage conversion is particularly useful when dealing with binary numbers that don’t lend themselves easily to grouping. By translating the binary number into the decimal system and then to hexadecimal, you gain a deeper understanding of the value you’re working with, even if it takes a bit longer.

We’ll delve into this method’s mechanics, beginning with the conversion of binary to decimal, followed by converting decimal to hexadecimal.

Converting Binary to Decimal

The first leg of the indirect conversion journey is all about decimal. To translate a binary number to decimal, you assign each binary digit a power of two, based on its position in the sequence, and then multiply. Summing up these products gives you the decimal number, a familiar figure that bridges the gap between binary simplicity and hexadecimal elegance.

It’s a conversion that pays homage to the binary system’s foundation while paving the way for the next stage of transformation.

Converting Decimal to Hexadecimal

With the binary digits now expressed in decimal form, the conversion to hexadecimal can commence. This process involves:

Dividing the decimal number by 16

Noting the remainders

Using the quotient for the next division until you’re left with zero

Reading the remainders in reverse order to get the hexadecimal number.

It’s a method that might seem roundabout compared to the direct approach, but it offers a valuable perspective on how numbers can traverse across different systems, each with its own rules and beauty.

Practical Examples of Binary to Hex Conversion

Having discussed the theoretical aspects of binary to hexadecimal conversion, it’s time to put theory into practice with real-life examples. By illustrating both the direct and indirect methods, these examples will solidify your understanding and give you the confidence to tackle binary to hexadecimal conversion in your own projects.

These examples will illustrate the conversion process in action, whether you’re preparing for an exam, tackling a programming task, or just fulfilling your intellectual curiosity.

Example 1: Direct Method

Let’s consider the binary number 110110111011. Using the direct method, we start by grouping the digits into sets of four from the right: 1101 1011 1011. Consulting our conversion chart, we find that 1101 corresponds to D, 1011 to B, and so on. As we combine these hexadecimal digits, we arrive at the final number: 6DB.

This example showcases the direct method’s efficiency in converting even complex binary numbers into their sleek hexadecimal form.

Example 2: Indirect Method

Consider the binary number 1001110, which translates to 78 in decimal. When we convert 78 to hexadecimal, we divide it by 16 to get 4 with a remainder of 14, which is E in hexadecimal. Proceeding with the division, we end up with 4E as the hexadecimal equivalent. This example illustrates the indirect method, where the decimal system serves as a stepping stone, ultimately leading to the hexadecimal translation of the original binary number.

Common Uses of Hexadecimal Numbers

Hexadecimal numbers are not just an academic exercise; they play a crucial role in various technical domains. From memory addressing in computing systems to defining colors in web design and aiding in debugging processes, the hexadecimal system’s utility is wide-reaching. Its ability to represent binary data in a compact format makes it an indispensable tool for programmers and engineers alike.

We will discuss some common applications wherein hexadecimal numbers are particularly beneficial.

Memory Addressing

In the computing world, hexadecimal numbers often serve as memory addresses, providing a simplified way to refer to specific locations in a computer’s memory. This is particularly useful when dealing with large memory spaces, where binary representations would be unwieldy.

By using hexadecimal, complex addresses are condensed into a more readable and manageable format, facilitating efficient memory management and access.

Color Codes in Web Design

Web designers are well-acquainted with hexadecimal color codes, a method of defining colors using 6-digit hexadecimal values. Each pair of digits represents the intensity of red, green, and blue, allowing for precise color specification. This standardized approach ensures that colors appear consistent across different devices and platforms, which is essential for creating harmonious and visually appealing designs.

Debugging and Data Representation

In the realm of debugging, hexadecimal numbers provide a clear representation of data that can help programmers identify and resolve issues. By presenting memory dumps and error messages in hexadecimal, developers can more easily interpret the raw data that underpins software behavior. This facilitates quicker diagnosis and resolution of problems, making hexadecimal an ally in the maintenance and optimization of computer programs.

Advantages of Using a Binary to Hex Converter Tool

While mastering binary to hexadecimal conversion manually is a valuable skill, the reality of modern computing is that efficiency and accuracy are paramount. This is where binary to hex converter tools like those found on PagesTools.com shine.

These tools offer:

Instantaneous conversions

User-friendly interface

Hassle-free experience

Error-free results

We’ll examine the unique benefits these converters offer.

Speed and Accuracy

Online binary to hex converters are designed to deliver results with incredible speed and accuracy. Engineered with advanced algorithms, these tools offer the following benefits:

Process large amounts of binary data in a blink of an eye

Ensure fast and error-free conversion

Free from the errors that can plague manual calculations

It’s the combination of rapid processing and precise algorithms that make these tools an invaluable asset for anyone working with binary data.

User-Friendly Interface

One of the hallmarks of a great tool is its ease of use, and binary to hex converters, like the hex conversion tool, are no exception. With interfaces that are intuitive and straightforward, these online utilities are accessible to both novices and experts.

A simple input field, a convert button, and clear instructions pave the way for a seamless conversion experience, ensuring that anyone can convert binary to hexadecimal without a steep learning curve.

Avoiding Calculation Errors

The risk of human error is ever-present in manual calculations, but binary to hex converter tools sidestep this issue. By automating the conversion process, these tools guarantee 100% accuracy, providing peace of mind that the results are reliable. This consistency is crucial, especially when working on critical applications where even a single mistake can have significant repercussions.

Summary

As we wrap up this journey through the world of binary and hexadecimal conversions, it’s clear that understanding and applying these concepts is key to navigating the digital landscape effectively. Whether opting for the direct grouping method or the indirect decimal route, the ability to convert binary to hexadecimal is an essential skill. And with the aid of user-friendly converter tools, this process is more accessible than ever. Embrace these methods and tools, and you’ll find yourself adept at translating the language of computers into a form that’s both comprehensible and practical.

Frequently Asked Questions

Why is the hexadecimal system used instead of binary for representing numbers in computing?

The hexadecimal system is used in computing because it offers a compact and human-readable representation of binary data, making it more accessible for humans to read and input large binary numbers. This simplifies complex computations.

What is the advantage of converting binary to hexadecimal using the direct method?

Converting binary to hexadecimal using the direct method is advantageous because it streamlines the process, saves time, and minimizes the risk of errors.

Can I convert binary to hexadecimal without using any tools?

Yes, you can convert binary to hexadecimal manually using direct or indirect methods, but using a tool like the Binary to Hex converter by PagesTools.com can provide quicker and more accurate results.

Are there specific cases where the indirect method of conversion is preferable?

Yes, the indirect method of conversion can be preferable when dealing with binary numbers that do not easily group into sets of four, or when a deeper understanding of the number's value is desired. This can be especially useful in complex numerical cases.

How do hexadecimal numbers help in debugging and data representation?

Hexadecimal numbers help in debugging by providing a clear and concise way to represent memory addresses, error codes, and raw data, allowing developers to identify and address issues more efficiently. This is because they offer a more compact representation of binary data, making it easier to work with.