Ultimate Bit Calculator: Effortlessly Convert Data Units in Seconds

When you need to convert bits to bytes, kilobytes, or any other unit of digital data, a bit calculator is your fast track to accuracy. Discard the complexity and make quick work of essential conversions as we guide you through the steps. Get ready to handle digital data with confidence.

Key Takeaways

Bits are the smallest unit of data in computing, forming the foundation of all digital communication and computing systems, with bytes consisting of 8 bits being the standard unit for data size and storage capacity.

The bit calculator is an essential tool for effortlessly converting between different units of data such as megabytes, gigabytes, terabytes, and petabytes, simplifying what could be a complex process of scaling up or down between these units.

Binary calculations and operations, including conversions between binary and decimal systems, are integral to understanding how digital devices process data, with bit calculators being pivotal for practical applications such as network bandwidth calculations and estimating storage requirements.

Understanding Bits and Their Importance in Computing

At the very heart of our digital world lies a deceptively simple concept: the bit. These fundamental data units are the basic unit of the digital realm, the binary bedrock upon which all forms of digital communication and computing systems are built. Whether you’re sending a text message, browsing the internet, or launching a spacecraft, bits are the linchpin, encoding all manner of data into the universal language of 0s and 1s.

This binary code is the essence of digital technology, and grasping its significance is the first step towards mastering the digital domain.

What Is a Bit?

In its purest form, a bit is the smallest unit of computer data storage, a single binary value that can represent a spectrum of binary states beyond mere numbers—such as yes and no, on and off, or true and false. These states are crucial for the digital logic that underpins the electronic systems we rely on every day.

Think of bits as the digital DNA, the source code that dictates how information is processed, stored, and interpreted in the binary system.

How Bits Relate to Bytes

While bits are the basic building blocks, bytes are the bricks that construct the edifice of digital data. A byte, made up of 8 bits, is the standard unit for file sizes and storage capacity. This might seem straightforward, but there’s a twist: not all bytes are created equal. Depending on system architecture or data format, the number of bits in a byte can vary, which can cause confusion when it comes to calculating file size and storage.

To add to the complexity, our digital lexicon distinguishes between bits and bytes using lowercase ‘b’ and uppercase ‘B’ respectively, as in ‘kb’ for kilobits and ‘KB’ for kilobytes.

The Binary System Unveiled

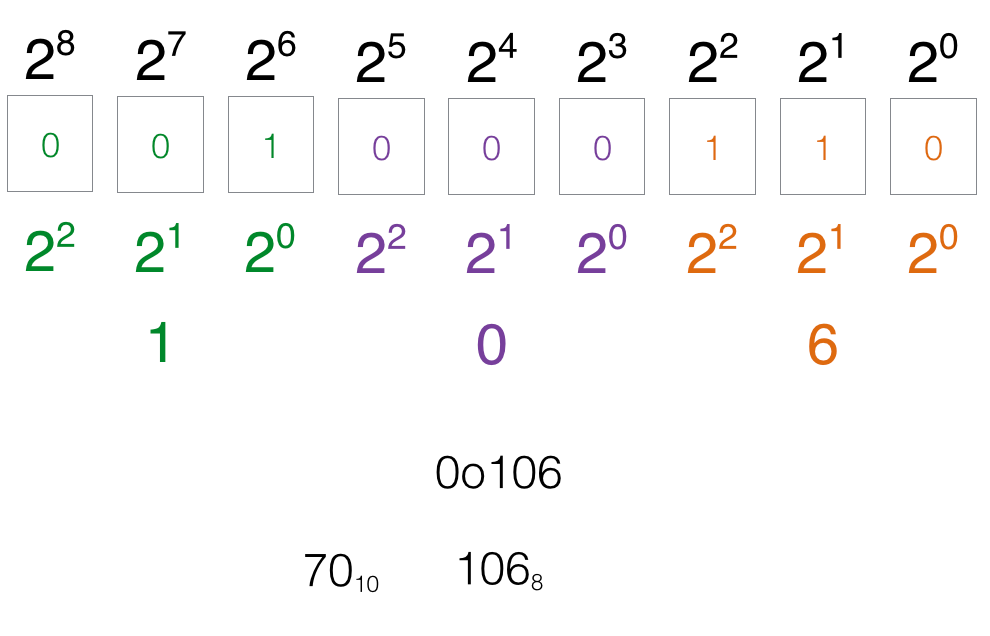
The binary system, with its base number of 2, stands in stark contrast to the base-10 decimal system ingrained in our everyday life. This international system, composed solely of 0s and 1s, is the cornerstone of binary logic, which governs everything from the simplest calculator to the most complex supercomputer.

Each move to the left in a binary sequence doubles the value—a simple, yet powerful progression that determines the place values in this base-2 number system. It’s this binary simplicity that allows for the sophisticated manipulation of data, optimizing performance in computing tasks.

Binary vs. Decimal: Understanding the Difference

The difference between binary and decimal systems is like comparing two different languages, each with its own rules and nuances. In binary, there’s no ‘2’; the sequence jumps from ‘1’ straight to ‘10’, reflecting its base-2 nature. This fundamental distinction is what sets apart binary calculations; where the decimal system scales by tens, binary scales by twos.

Understanding this divergence is key to grasping how digital devices interpret and process the vast array of data they encounter.

Reading and Writing Binary Numbers

Binary numbers, when decoded correctly, correspond to specific decimal numbers. For instance, the binary ‘1010’ is the decimal ‘10’, with each position representing an exponential increase in value. A helpful unit for interpreting binary numbers is the ‘nibble’, a group of four bits, or half a byte.

The concept of nibbles not only aids in reading binary sequences but also serves as the basis for understanding how data is organized at the bit level.

Using a Bit Calculator for Conversions

Diving into the world of digital storage units can be overwhelming, but here’s where a bit calculator comes to the rescue. This tool is designed to effortlessly convert bits into familiar data measurements like:

megabytes

gigabytes

terabytes

petabytes

Making it indispensable for anyone working with digital data, especially when dealing with the third column.

Whether you’re sizing up a file or calculating data transfer rates, a bit calculator—such as the one by PagesTools.com—provides a user-friendly interface to navigate these conversions with ease.

Converting Bits to Other Units

The versatility of a byte converter, such as a bit calculator, shines when you need to scale bits to larger data units, such as kilobytes or terabytes. By multiplying the number of bits by the appropriate factor, a mundane task is transformed into a simple click or keystroke. The calculator can handle a range of units, scaling up by factors of 1,024 to convert bytes, and then dividing by a similar factor to convert kilobytes to the desired larger unit, such as megabytes or gigabytes. With this tool, you can easily convert bytes and ensure your data is accurately represented.

This process, which can be facilitated by a binary bytes reference table, simplifies what could otherwise be a complex mathematical endeavor.

Calculating File Size and Data Transfer Rates

The bit calculator is more than just a conversion tool; it’s a vital instrument for determining file sizes and data transfer rates. By factoring in the size of a file along with your internet connection speed, the calculator computes the time needed for data transfer, thus providing a clear picture of bandwidth and storage requirements.

To calculate data transfer rates, follow these steps:

Multiply the file size in megabytes by 8 to convert it to megabits.

Use the “convert megabytes” step by multiplying the result by 1,024 twice to convert to bits.

Divide the final result by the transfer time in seconds.

Deciphering Data Unit Symbols and Their Values

Understanding the symbols and values associated with data units is crucial for accurately assessing storage capacities and data magnitudes in computing. The hierarchy of units progresses from the bit to the byte and beyond, with each jump in magnitude signifying a substantial increase in data quantity. Recognizing these units and their respective symbols ensures clarity when dealing with file sizes, storage capacities, and the vast seas of digital information that we navigate daily.

Recognizing Unit Symbols

In the world of computing and data storage, understanding the unit symbol, like kB, MB, and GB, is crucial. These symbols represent the hierarchy of data units, with each indicating a specific multiple of bytes. They are part of a sequence where each unit is 1,024 times larger than the previous one, from kilobytes to exabytes. Recognizing these symbols is critical for understanding the data magnitude they represent, which is essential in various computing and data storage activities.

Memory sizes in information technology also include exabyte (EB), zettabyte (ZB), and yottabyte (YB), which are used to denote extremely large data capacities typically found in massive data centers and scientific research.

How Much Data Is in a Megabyte vs. a Gigabyte?

Understanding the difference between a megabyte and a gigabyte is about more than just numbers; it’s about recognizing the scale of data we’re working with. Here are some key differences:

A megabyte is a million bytes

A gigabyte is a billion bytes—a thousandfold difference

In the binary system, these units are even larger, with a mebibyte being 1.048576 megabytes and a gibibyte exceeding a gigabyte

The implications of these differences become increasingly significant as we deal with larger units like terabytes and petabytes, especially when dealing with large datasets.

When it comes to computing and data storage, accurately grasping these capacities in the same manner is tantamount to maximizing efficiency and performance.

Step-by-Step Guide to Binary Conversions

Converting between binary and decimal systems might seem daunting, but it’s a process that can be mastered with a methodical approach. Binary conversions involve multiplying binary digits by their corresponding powers of 2 and summing the results, a process that’s unique to binary arithmetic.

Mastery of binary conversions opens the door to a deeper understanding of how digital devices process and represent data. It also paves the way for advanced binary operations like:

Addition

Subtraction

Multiplication

Division

From Decimal to Binary

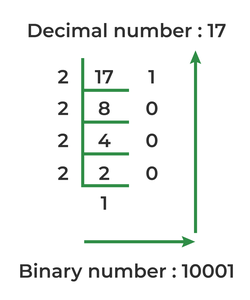
The conversion from decimal to binary is a journey of division and documentation. By dividing the decimal number by 2 and noting the remainders, then writing these remainders in reverse order, a decimal number is transformed into its binary counterpart. This process is akin to unraveling the decimal number into its binary building blocks, revealing a sequence that starts with 1 for the decimal number ‘1’ and grows exponentially to ‘1010’ for the decimal number ‘10’.

The binary code that emerges is not just a random string of 0s and 1s; it’s a calculated representation of a decimal value in the language of binary.

From Binary to Decimal

Reversing the conversion process, from binary to decimal, involves multiplying each binary digit by its corresponding power of 2 based on its position in the binary number. The sum of these products yields the decimal equivalent of the binary number, a process that can be streamlined using the doubling method.

Starting from the leftmost digit, each digit is doubled and added to the next, continuing until the final sum is reached. This method is a testament to the elegance of binary logic, where complex digital phenomena can be distilled into straightforward arithmetic.

Advanced Binary Operations Made Simple

Delving into advanced binary operations doesn’t have to be intimidating. These operations, while based on the same principles as those in the decimal system, are simplified by the use of only two digits—0 and 1. Whether it’s binary addition and subtraction, or the more complex multiplication and division, each operation follows a logical and methodical process that, once understood, can be performed with relative ease.

For anyone looking to delve deeper into the world of computing or simply to understand the mechanics behind their digital devices, these operations are the tools of the trade.

Binary Addition and Subtraction

Binary addition and subtraction are the keystones of binary arithmetic. In addition, when the sum of two digits equals 2, a carryover is triggered, much like when adding large numbers in the decimal system. This process is mirrored in subtraction, where borrowing is necessary whenever 1 is subtracted from 0.

These operations may seem familiar in concept, but the binary system’s restriction to two digits introduces a unique twist to the process, making it a fascinating study of numerical simplicity and efficiency.

Binary Multiplication and Division

Binary multiplication and division, while mirroring the steps of their decimal counterparts, are simplified by the binary system’s two-digit nature. Multiplication involves a process of addition and shifting, where multiplying by 1 maintains the original number, and multiplication by 0 results in a simple zero.

Binary division is akin to long division but uses binary subtraction at its core, requiring a solid grasp of binary subtraction for accurate calculation.

Maximizing Storage: Understanding Byte Multiples

In the realm of digital storage, understanding byte multiples from kilobytes to exabytes is akin to knowing the right ingredients for a recipe. By efficiently utilizing these multiples, one can tailor storage solutions to specific needs, avoiding wastage and optimizing performance. This knowledge is not merely technical; it’s a practical asset that becomes increasingly beneficial as the size of datasets grows, scaling up the memory savings and ensuring that storage capacity is used in the most strategic and cost-effective way.

Binary Multiples: Kibibytes and Mebibytes

The binary system intricately weaves multiples like kibibytes and mebibytes, which are based on powers of 1024, offering a different perspective compared to the decimal system’s reliance on powers of 1000. A kibibyte (KiB) equals 1024 bytes, and a mebibyte (MiB) equals 1,048,576 bytes or one megabyte, reflecting the binary system’s precise structure for quantifying data.

These binary multiples, including the kilobyte (KB) and megabyte (MB), define the capacity of digital storage, and understanding the distinction between binary and decimal measurements is essential for anyone dealing with computing devices to assess storage accurately.

Converting Between Binary and Decimal Multiples

Navigating between binary and decimal multiples is a task that bit calculators simplify, bridging the gap between two systems of data quantification. To convert from binary to decimal multiples, one must multiply or divide by 1024 for each step up or down the binary ladder. This conversion is crucial for understanding the actual storage capacity of digital devices, as the difference between binary and decimal measurements can be significant.

Bit calculators play a pivotal role in such conversions, offering a reliable and user-friendly way to determine the true size of files and storage mediums.

Common Use Cases for a Bit Calculator

Bit calculators are indispensable tools that serve a variety of practical purposes beyond simple conversions. From network engineers calculating bandwidth requirements to individuals assessing their digital storage needs, the bit calculator is a vital ally in a world governed by binary data. Its ability to execute complex binary calculations quickly and precisely is crucial for maintaining efficiency and ensuring accuracy in various professional settings.

Whether it’s planning digital infrastructure or optimizing storage solutions, the bit calculator is a cornerstone of digital proficiency.

Network Bandwidth Calculations

In the dynamic field of network engineering, bit calculators are essential for calculating the bandwidth needs for VoIP calls and other data-intensive applications. By considering variables such as codec types, bit rates, and sample sizes, network engineers can determine the precise bandwidth required for optimal performance. These calculations take into account the specific codec, whether it’s G.711, G.729, or G.722, each with its own set of requirements for delivering clear and reliable voice communication.

The total bandwidth is calculated by multiplying the packet size by the number of packets transmitted per second, a process that a bit calculator can handle effortlessly.

Estimating Storage Requirements

Estimating storage requirements is another realm where bit calculators prove their worth, especially when dealing with uncompressed raster image files or large video projects. These calculators help translate binary data, representing image resolution and bit depth, into understandable quantities, enabling users to plan their storage needs accordingly.

Whether it’s for personal use or within a professional setting, having the ability to accurately gauge how much data will be generated, and therefore how much storage will be needed, is vital for efficient data management.

Summary

As we wrap up this digital odyssey, it’s clear that bits and the binary system are more than just technical jargon—they are the lifeblood of our digital existence. From the simplicity of a single binary value to the complexity of data unit conversions, understanding this binary landscape is essential for anyone looking to navigate the digital world with confidence. Whether it’s through the use of a bit calculator or by internalizing the principles of binary operations, the power to harness these fundamental units of data is within your grasp. Embark on this journey of discovery, and unlock the full potential of your digital interactions.

Frequently Asked Questions

What exactly is a bit and why is it important?

A bit is the smallest unit of data in a computer system, represented as either a 0 or a 1. It's important because it's the foundation of all digital data and computing systems, encoding everything from text to images to complex software operations.

How do bits relate to bytes, and why does it matter?

Understanding the relationship between bits and bytes is important because 1 byte equals 8 bits, and bytes are the standard units used for file sizes and storage capacity, which helps in accurately assessing storage needs.

Can you explain the difference between the binary and decimal systems?

The binary system uses 2 digits (0 and 1) and scales by powers of 2, while the decimal system uses 10 digits (0 through 9) and scales by powers of 10, impacting how computers process and represent data.

What are some common uses for a bit calculator?

A bit calculator is commonly used for tasks such as converting binary values, calculating file sizes, data transfer rates, and network bandwidth requirements. It is a versatile tool for managing data-related calculations.

How does binary multiplication differ from decimal multiplication?

Binary multiplication is simplified compared to decimal multiplication because it uses only two digits, 0 and 1, which makes the process of addition and shifting more straightforward and streamlined.