Best Methods to Convert Decimal to Binary: Formula, Table & Examples

Want to convert decimal to binary? This guide explains the steps with simple examples. Let’s dive into decimal to binary conversion.

Key Takeaways

The conversion from decimal to binary is fundamental in computing, involving a methodical approach known as the division by 2 method for accuracy and fluency in digital processes.

Decimal and binary systems operate differently: the decimal system uses ten digits (0-9), while the binary system uses two digits (0 and 1), making the binary system crucial for computing tasks.

Understanding decimal to binary conversion is essential across various fields such as computer programming, digital communications, and encryption, highlighting its widespread practical applications and importance in technology.

Introduction

Dive into the fascinating world of number systems, where we translate the numbers we use daily into a form that computers can comprehend. The conversion from the decimal to the binary number system is more than a mere academic exercise; it’s a critical process that underpins programming, data storage, and digital communication.

By mastering this skill, one can unlock a deeper understanding of how digital devices operate and process information in a language composed solely of binary digits.

Understanding Number Systems

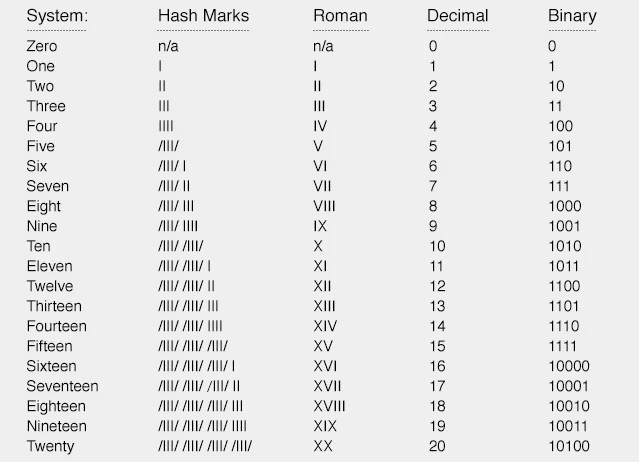
At the heart of digital technology lies a fundamental understanding of number systems. While the decimal number system, with its ten digits, is second nature to us, the binary system operates on an entirely different premise. With just two digits, 0 and 1, the binary number system forms the backbone of all computing processes.

Grasping the conversion between these two systems is not just a mathematical endeavor but a step towards fluency in the language of technology.

Decimal Number System Definition

The decimal number system, also known as the base-10 system or the hindu arabic number system, is the universal language of numbers used by humans across cultures and centuries. It’s characterized by ten distinct symbols ranging from 0 to 9, each representing a unique value.

When we count, perform calculations, or express quantities, we’re utilizing the decimal system—a testament to its ingrained role in our daily lives and the importance of understanding decimal value.

Binary Number System Definition

The binary number system, also known as base-2, is composed of only two binary digits: 0 and 1. These two digits are used to represent all numerical values in the system. Each binary digit, or bit, represents an exponential power of 2, with the rightmost digit being the most significant.

This simplicity makes the binary system ideal for computing and digital electronics, where it has become the fundamental language through which all digital information is processed and stored.

Steps to Convert Decimal to Binary

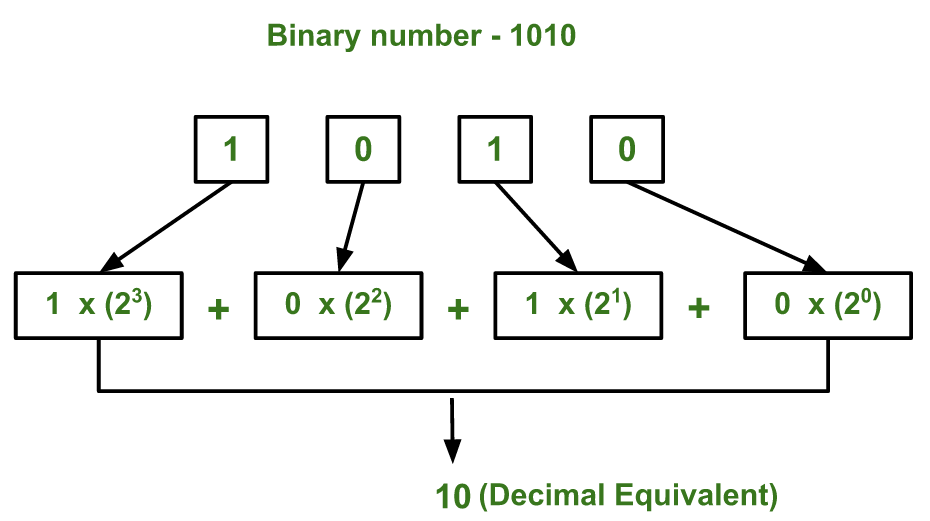
The translation of decimal numbers to binary equivalents involves a methodical approach known as the division by 2 method. This technique requires dividing the decimal number by 2, noting down the remainder, and repeating the process with the quotient until it reduces to zero.

The binary number is then derived by arranging the remainders in reverse order, starting from the last remainder obtained.

Decimal To Binary by PagesTools.com

PagesTools.com offers a seamless experience for those looking to convert decimal numbers to binary. This process, which involves changing the base of a number from 10 to 2, is made simple with online tools that automate the conversions, providing instant results and eliminating the potential for human error.

Division Method

Utilizing the division method for binary conversion involves the following steps:

Start by dividing the decimal number by 2.

Note the remainder of this division.

Use the quotient as the new number to be divided by 2.

Repeat this process until the quotient reaches zero.

At the end of the division process, the binary equivalent is determined by writing the remainders in reverse order.

The last remainder represents the least significant bit.

Example Conversion

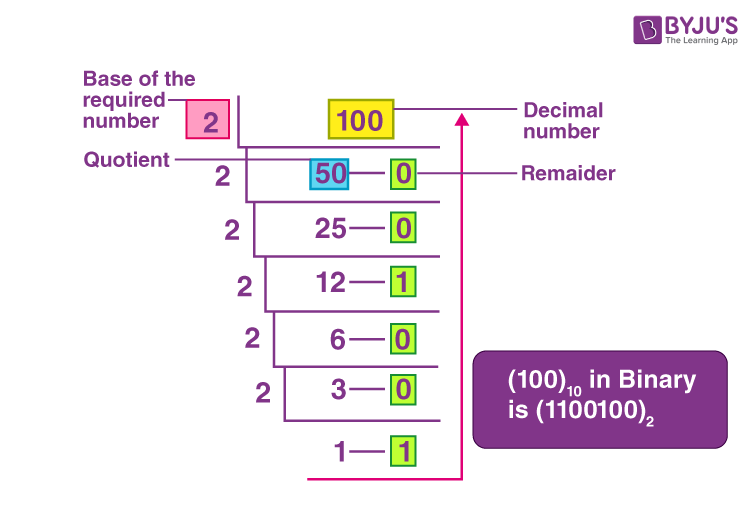
For instance, converting the decimal number 13 to binary is a straightforward process. Here are the steps:

Divide 13 by 2 to get a quotient of 6 and a remainder of 1.

Divide 6 by 2 to get a quotient of 3 and a remainder of 0.

Divide 3 by 2 to get a quotient of 1 and a remainder of 1.

Divide 1 by 2 to get a quotient of 0 and a remainder of 1.

Writing these remainders in reverse order, we obtain the binary number 1101, which is the binary equivalent of the decimal number 13.

Converting larger numbers follows the same principle. Take the decimal number 45 as an example. The first division by 2 gives a quotient of 22 and a remainder of 1. Continuing this process until the quotient is zero, we collect the remainders and then write them in reverse order to obtain the binary number 101101, which represents the decimal number 45 in binary form.

The division method ensures accuracy and provides a systematic way of achieving the conversion, with each step building upon the previous one. By practicing this method, one can swiftly convert any decimal number to its binary equivalent with confidence.

Decimal to Binary Conversion Table

A decimal to binary conversion table serves as a handy reference, displaying the equivalent binary values for decimal numbers. This table is particularly useful for beginners who are still familiarizing themselves with the patterns and relationships between the two number systems.

It also serves as a quick-check guide for those who need to confirm their manual conversions.

First 20 Whole Numbers

Such a table typically includes the binary equivalents for the first 20 whole numbers, providing a clear visual representation of the conversion process. For instance:

The number 1 in decimal is 1 in binary

The number 2 is 10 in binary

The number 3 is 11 in binary

The number 4 is 100 in binary

The number 5 is 101 in binary

As we move up the table, the binary numbers increase in length, reflecting the exponential nature of the binary system.

Key Patterns and Insights

Analyzing the conversion table reveals key patterns, such as the observation that binary numbers corresponding to even decimal numbers end in 0, while those for odd numbers end in 1. This pattern is consistent throughout the table and is a direct result of the division by 2 method used in the conversion process.

Converting Decimal Fractions to Binary

Converting decimal fractions to binary requires a slightly different approach than that used for whole numbers. The process involves separating the number into its integral and fractional parts, converting each part independently, and then combining them to form the binary equivalent.

This method ensures that both whole units and partial units are accurately represented in the binary system.

Integral and Fractional Parts

In a decimal number, the integral part is located before the decimal point and represents whole numbers, whereas the fractional part follows the decimal point and represents the fractional values. The integral part is converted using the division by 2 method, and the fractional part is handled through repeated multiplication by 2. The results of these conversions are then combined, with the integral part placed before the binary point and the fractional part after.

Example Conversion

To illustrate, let’s convert the decimal fraction 0.125 to binary. Start by multiplying 0.125 by 2, resulting in 0.25 and taking the integral part, which is 0. Repeat this process with the fractional part 0.25 to get 0.5, and again with 0.5 to get 1.0. The integral parts obtained are 0, 0, and 1, which gives us the binary equivalent of 0.001 for the decimal fraction 0.125.

For a more complex example, consider the decimal number 10.2. First, we convert the number 10 to binary, which is 1010. Then, we tackle the fractional part 0.2, which through the process of repeated multiplication by 2, yields a binary fraction of 0.0011. Combining the two parts, we obtain the binary equivalent of the decimal number 10.2 as 1010.0011. This example underscores the importance of addressing each part separately to ensure accuracy in the conversion.

Common Questions and Examples

Navigating the conversion from decimal to binary can prompt various questions, particularly when dealing with specific numbers. To demystify the process, let’s explore some common inquiries by walking through examples of decimal numbers and their binary equivalents.

What is the Binary Equivalent of Decimal 97?

Finding the binary equivalent of decimal 97 is a matter of applying the division by 2 method. Starting with 97, we divide by 2 to obtain a quotient of 48 and a remainder of 1. Continuing this process, we eventually write down the remainders in reverse order to arrive at the binary equivalent of 97, which is 1100001.

How to Convert Decimal 254 to Binary?

To convert decimal 254 to binary, we again employ the division by 2 method. By dividing 254 by 2 repeatedly and recording the remainders, we construct the binary number bit by bit. Once the quotient is zero, we arrange the remainders in reverse order to reveal the binary equivalent of 254:

1

1

1

1

1

1

1

0

So, the binary equivalent of 254 is 11111110.

Practice Problems

To solidify your understanding of binary conversion, try converting decimal 29 to binary as a practice problem. This exercise will not only test your grasp of the conversion process but also enhance your speed and accuracy, which are critical for practical applications and exams.

Applications of Decimal to Binary Conversion

The applications of decimal to binary conversion span various fields, including:

Computer programming

Digital communication

Encryption

Image processing

Understanding this conversion is not just an academic requirement but a practical skill that is widely utilized in the technology-driven world we live in.

Importance in Computing

In the realm of computing, binary numbers and their binary value representation are essential for the efficient processing and storage of data. Binary allows computers to interpret electrical signals as on and off states, enabling the execution of complex computational tasks.

Moreover, cryptographic algorithms often rely on binary conversion to secure data through encryption and decryption processes.

Real-World Examples

In real-world scenarios, binary conversion plays a pivotal role in various applications, such as:

Network communications, where data packets are encoded in binary for transmission

Digital images and graphics, which are represented in binary code to handle pixels and color values effectively

Email communication, where emails are converted into binary before they traverse the vast networks connecting us to the rest of the world.

Summary

To conclude, the journey from the decimal numbers we use daily to the binary digits that fuel our digital devices is both fascinating and fundamental. By mastering the methods of conversion, one acquires a valuable skill set that is applicable in numerous technological fields. Embrace the simplicity and precision of binary, and you’ll unlock a new dimension of digital literacy.

Frequently Asked Questions

What is the most significant bit in a binary number?

The most significant bit in a binary number, also known as the MSB, is located at the leftmost position and represents the highest value in the binary representation.

Can binary numbers represent decimal fractions?

Yes, binary numbers can represent decimal fractions by using a point similar to a decimal point, with binary digits to the right representing fractional values.

Why do binary numbers use only two digits?

Binary numbers use only two digits, 0 and 1, because they correspond to the two states of an electrical signal—off and on—which is essential for digital electronics to process and store data.

Is there a quick way to convert decimal numbers to binary?

Yes, using online tools like PagesTools.com can offer a quick and error-free way to convert decimal numbers to binary.

How does binary conversion apply to digital communications?

Binary conversion is essential in digital communications as it allows information to be encoded into binary data for efficient transmission and storage, ensuring accurate delivery across digital networks.