Simple Guide: Convert Hex to Binary with Examples

Need to convert hex to binary? You’re in the right place. This guide will show you how each hexadecimal digit translates to four binary digits effortlessly. We’ll cover the steps, examples, and useful tools to make your conversion quick and accurate.

Key Takeaways

Hexadecimal to binary conversion is straightforward due to the direct relationship where each hexadecimal digit maps to four binary digits.

PagesTools.com offers an efficient online tool for converting hexadecimal numbers to binary, useful for both single digits and large files.

Understanding both direct and indirect methods of conversion can enrich comprehension of how hexadecimal and binary systems interrelate, enhancing problem-solving skills in various computing applications.

Introduction

The magic of hexadecimal to binary conversion lies in its simplicity and symmetry. Each hexadecimal digit corresponds to four binary digits, creating a beautiful, streamlined process for translation between the two. This represents a harmonious balance where the expansive language of hexadecimal—with its symbols ranging from ‘0’ to ‘F’—is distilled into the binary digits 0 and 1, the very essence of computer logic.

Understanding this conversion is not just a theoretical exercise; it’s a practical skill that is instrumental in various aspects of computing, from viewing memory registers to debugging applications. With each step in this guide, you’ll see how these systems interlink and why mastery over them is equal parts art and science.

Hex To Binary by PagesTools.com

It’s worth noting that at times, we require swift outcomes without the hassle of manual computations before we delve deeper into the intricacies of manual conversion. Enter PagesTools.com, a beacon of efficiency in a world teeming with data. This online haven simplifies the task of converting hexadecimal numbers to their binary equivalents with just a few clicks.

Whether you’re grappling with a single hexadecimal digit or wrestling with an entire file of hex numbers, PagesTools.com stands ready to transform them into binary numbers with ease and precision. The versatility of PagesTools.com is evident in its ability to cater to different user needs. You can enter your hexadecimal number manually or upload a file for a batch conversion, saving you valuable time and ensuring accuracy.

The site epitomizes the seamless integration of technology in our daily tasks, providing a binary conversion table that acts as a bridge between the abstract world of hexadecimal digits and the concrete reality of binary numbers.

Understanding Hexadecimal and Binary Number Systems

An appreciation of the beauty of hexadecimal to binary conversion necessitates a foundational understanding of these number systems. The binary number system, or base-2, is the DNA of computer systems, composed of just two symbols—0 and 1, known as bits. These bits are the atoms of digital data, representing the on and off states that computers interpret to perform operations. On the other hand, the hexadecimal number system, or base-16, employs sixteen symbols ranging from 0 to 9 and A to F. This system was devised as a more human-friendly representation of binary data, allowing us to succinctly express long strings of binary digits.

The process of converting hexadecimal to binary essentially involves a translation from one digital language to another. Each hexadecimal digit is equal to four binary digits, a relationship that simplifies the conversion process. Thus, a single hex digit can represent the same amount of information as four binary digits, consolidating the binary language into a more digestible form for human interaction. This direct correlation paves the way for efficient conversion methods, which we will explore next.

Steps to Convert Hexadecimal to Binary

There are two main methods to approach the conversion from hexadecimal to binary: the direct method, which offers a quick translation by replacing each hexadecimal digit with its four-bit binary equivalent, and the indirect method, which requires an intermediate step of converting to the decimal number system first. Both approaches arrive at the same destination—the equivalent binary number—but they offer different journeys to get there.

Whether you favor the efficiency of the direct method or the methodical nature of the indirect approach, mastering both techniques ensures you’re well-prepared for any conversion task.

Direct Method: Conversion Using Binary Digits

Converting hexadecimal to binary directly is somewhat like decrypting a secret message—each hexadecimal digit holds a predefined binary code waiting to be revealed. It’s a straightforward substitution game: every hexadecimal digit from 0 to F has a corresponding four binary digits sequence. This method bypasses the need for any intermediate steps, allowing for an instant conversion that’s both time-efficient and satisfying.

Imagine you’re given a hexadecimal number—let’s say ‘B3’. Using the direct method, you’d translate ‘B’ to its four-bit equivalent ‘1011’ and ‘3’ to ‘0011’. The resulting binary number ‘10110011’ is a direct transcription of the original hex number. This approach is particularly useful for those who enjoy pattern recognition and have a penchant for puzzles. It’s a quick, reliable way to bridge the gap between the hexadecimal system and the binary language that underpins all computer operations.

Indirect Method: Conversion via Decimal System

Converting hexadecimal to binary indirectly involves a detour through the decimal number system, offering a different perspective on the translation process. This method may appeal to those who find comfort in the familiarity of decimal numbers—a system we use in our daily lives.

The process of converting a hexadecimal number to decimal and then to binary involves the following steps:

Interpret the given hexadecimal number as a series of place values, each multiplied by powers of 16.

Calculate the sum of these multiplications to obtain the decimal equivalent.

Methodically convert the decimal number to binary by continuously dividing by 2 and noting the remainders.

By following these steps, you can successfully convert hex and binary convert hexadecimal to a hexadecimal number.

For example, converting the hexadecimal number ‘4E’ to binary would involve the following steps:

Turn ‘4’ into 4 and ‘E’ into 14 (since E represents 14 in decimal).

Calculate the decimal equivalent: 4*16 + 14 = 78.

Divide 78 by 2 repeatedly, noting the remainders, until we reach 0.

The binary equivalent is then read in reverse order of the remainders.

While this method may not be as rapid as the direct one, it provides a deeper understanding of the relationship between hexadecimal, decimal, and binary systems. It’s a testament to the versatility of number conversion and the interconnectedness of these seemingly disparate number systems.

Hexadecimal to Binary Conversion Table

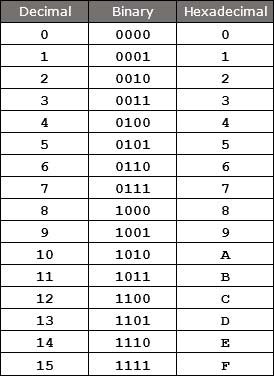
A hexadecimal to binary conversion table in your possession acts like a secret key, unlocking the binary counterparts of hexadecimal digits. This table serves as a quick reference guide, neatly displaying the binary representations of hexadecimal digits from 0 to F. Each entry in the table is like a portal, instantly revealing the four binary digits that encapsulate the value of its hexadecimal counterpart.

The conversion table is not only a practical tool but also a visual representation of the relationship between the hexadecimal and binary systems. For instance, the hexadecimal digit ‘A’ finds its binary alter ego in ‘1010’, while ‘F’ translates to ‘1111’. This table is especially handy for beginners, as it provides a clear and concise map for navigating the conversion process without having to memorize each correspondence. With this table, the conversion from hexadecimal to binary becomes a matter of matching symbols, akin to finding the right piece in a puzzle.

Examples of Converting Hexadecimal to Binary

Practical examples will help cement the understanding of the conversion process. Imagine you’re faced with the hexadecimal number ‘1C3’. Using the direct method, you would replace ‘1’ with ‘0001’, ‘C’ with ‘1100’, and ‘3’ with ‘0011’, resulting in the binary number ‘000111000011’. This method is brilliantly efficient for small numbers, providing a clear path from hexadecimal digits to binary language.

But what about larger numbers, or when you’re dealing with more complex conversions? The indirect method shines in these situations. Let’s take the hexadecimal number ‘7A9’. Converting ‘7’ to 7, ‘A’ to 10, and ‘9’ to 9, you’d then calculate the decimal equivalent (716^2 + 1016 + 9 = 1961). The subsequent conversion to binary involves dividing 1961 by 2, yielding a series of remainders that, when read in reverse order, give us the binary number ‘011110101001’. This example showcases the indirect method’s thoroughness and its ability to handle conversions that might seem daunting at first glance.

In both methods, the process is methodical and precise, turning the art of conversion into a science. Whether you prefer the direct or indirect approach, the end result is the same—a binary number that accurately represents the original hexadecimal value. These examples are stepping stones, guiding you toward mastery of the conversion techniques.

Converting Hexadecimal Numbers with Decimal Points

The process of converting hexadecimal numbers to binary extends beyond integers, becoming more complex with the introduction of decimal points. However, fear not, as the core principles remain the same. When faced with a hexadecimal number containing a decimal point, such as ‘2.C4’, you convert each digit to binary while maintaining the decimal structure. Trailing zeros after the decimal point are disregarded, as they do not affect the value.

For example, converting ‘1.B3’ to binary would involve translating ‘1’ to ‘0001’, ‘B’ to ‘1011’, and ‘3’ to ‘0011’, resulting in the binary number ‘0001.10110011’. The decimal point in the binary number is placed in the same position relative to the digits as it is in the hexadecimal number, ensuring the values on either side of the point are accurately represented. This technique extends the utility of hexadecimal to binary conversion beyond whole numbers, encompassing the full spectrum of numerical values used in computing.

Practice Problems on Hexadecimal to Binary Conversion

By practicing, theoretical concepts become instinctive. To hone your skills in hexadecimal to binary conversion, engage with a set of practice problems designed to challenge and reinforce your knowledge. These problems come complete with answers, allowing you to self-assess and ensure your mastery of the conversion process. Whether you’re a student seeking to excel in digital electronics or a professional brushing up on your skills, these practice problems are the perfect companion.

Consider the hexadecimal number ‘5D3’. Convert it to binary using either the direct or indirect method, and then check your answer against the solution provided. By working through these problems, you’ll not only become more proficient in conversions but also gain confidence in your ability to tackle the numerical aspects of computing systems. The practice problems serve as a bridge between learning and doing, solidifying your understanding through hands-on application.

Applications of Hexadecimal to Binary Conversion

The examination of the hexadecimal to binary conversion isn’t complete without acknowledging its numerous uses in technology’s broad spectrum. This conversion is not just an academic exercise; it’s a critical tool in the toolbox of anyone working in computing systems, networking, or software engineering. Hexadecimal numbers are often used to represent data more compactly in programming languages, while binary is the lifeblood of digital electronics, dictating how circuits function and interact.

One of the most practical uses of hexadecimal to binary conversion is in the realm of debugging and memory allocation. Here, hexadecimal notation serves as a map to the values stored in memory locations, offering insights into the inner workings of a program. By converting these values to binary, engineers and developers can peer into the binary language that dictates the behavior of their creations, enabling them to troubleshoot issues and optimize performance. The conversion process is a bridge between the abstract and the tangible, a tool that brings clarity to the complex interactions within computer systems.

Summary

As we draw this guide to a close, let’s reflect on the journey we’ve undertaken. From the fundamental principles underlying the hexadecimal and binary number systems to the practical steps of conversion, we’ve navigated through the intricacies of a skill that is as much about understanding the language of computers as it is about the elegance of mathematics. The conversion methods, tables, examples, and practice problems provided here serve as a roadmap, guiding you to become fluent in this essential aspect of computing.

Whether you’re a student embarking on a career in technology, a seasoned professional looking to refresh your knowledge, or simply a curious mind exploring the foundations of digital data, the ability to convert hexadecimal to binary is a valuable skill. It’s a testament to the beauty of numbers and their power to shape the world we live in. May this guide serve as a beacon, illuminating the path to mastery and inspiring you to delve deeper into the fascinating world of computing.

Frequently Asked Questions

Why do we need to convert hexadecimal numbers to binary?

Converting hexadecimal to binary is necessary because computers only understand binary language, and it allows for easier storage and processing of data within computer systems. Hexadecimal provides a compact form for representing binary data, making it more human-readable.

What is the direct method of converting hexadecimal to binary?

To convert hexadecimal to binary using the direct method, simply replace each hexadecimal digit with its corresponding four-bit binary representation. It's a quick and straightforward process that doesn't require any intermediate conversions.

Can I convert hexadecimal numbers with decimal points to binary?

Yes, you can convert hexadecimal numbers with decimal points to binary by converting each digit while maintaining the decimal structure, and ignoring trailing zeros after the decimal point.

Is there a tool that can help me convert hexadecimal to binary?

Yes, PagesTools.com offers a tool to convert hexadecimal to binary.

What are some practical applications of hexadecimal to binary conversion?

Hexadecimal to binary conversion has practical applications in computing systems, networking, digital electronics, and programming languages, making it essential for memory and register value display, addressing, circuit design, and data representation. It is utilized in various fields for these crucial purposes.