Comprehensive Probability Calculator for Accurate Results

Need to calculate event probabilities quickly and accurately? Our Probability Calculator helps you do just that. Ideal for betting, academics, or any situation requiring odds calculation, this tool simplifies the math. This article guides you on using it effectively and understanding the core concepts behind probability.

Key Takeaways

The Odds Probability Calculator by PagesTools.com converts odds into significant probability values, aiding bettors and analysts in making informed decisions by providing clear insights into chances of success.

Probability calculations can be simplified with tools like the Probability Calculator, which supports both simple and complex problems, including determining probabilities for both independent and dependent events.

Understanding different types of probability (theoretical vs. experimental) and probability distributions (discrete vs. continuous) is crucial for real-world applications like meteorology, finance, sports, and healthcare, where probability helps make informed decisions and accurate predictions.

Introduction

Probability permeates various aspects of life, from the simple toss of a coin to the complexities of predicting weather patterns, assessing insurance risks, and making strategic business decisions. Serving as a potent tool, probability quantifies uncertainty, thereby offering a structure to comprehend the randomness that surrounds us.

The Odds Probability Calculator enables the conversion of odds into significant probability values, thereby transforming raw data into lucid insights. This tool is particularly handy for bettors and analysts, offering an easy-to-understand percentage that aids in informed decision-making. After all, understanding probability is not just about crunching numbers—it’s about gaining a deeper understanding of the world and making smart choices.

Understanding Probability Calculations

Why is probability important? Primarily, it assists in understanding uncertainty. Probability enables anticipation and readiness for future events by facilitating the forecast of weather and prediction of market trends. It’s like having a crystal ball that, while not perfect, can provide a reliable glimpse into the future.

How is probability calculated? The process is surprisingly straightforward. The Odds Probability Calculator is a tool that helps in converting odds into probability and determining the percent chance of winning and losing. It is designed to simplify the process for users. By entering the odds for winning, users get clear insights into their chances of success. This simple yet powerful tool, can help anyone—from seasoned analysts to casual bettors—navigate the uncertain waters of probability.

Definition of Probability

So, how can we define probability? In simple terms, it measures the likelihood of a specific event happening. It’s quantified as a number between 0 and 1, where 0 represents an impossible event and 1 represents a certain event. Though this might sound abstract, it carries tangible implications in our day-to-day lives.

For instance, if a weather forecast predicts a 70% chance of rain while you’re planning an outdoor event, it might be wise to consider an indoor venue or prepare a backup plan. Here, 70% is the probability of rain—a quantifiable measure of an uncertain future event. Understanding this concept is the first step towards mastering the art of probability.

Types of Events: Independent and Dependent

In the world of probability, events are classified as independent or dependent. Independent events are events where the outcome of one event has no impact on the outcome of another event. This means that the occurrence of one event does not affect the other. Imagine tossing a fair coin twice. The outcome of the first toss doesn’t affect the second, making these independent events.

On the other hand, dependent events are intertwined—the occurrence of one event influences the other, such as event b. Consider the game of blackjack. The value of the first drawn card can significantly affect the probability of the subsequent draws, making these dependent events. Understanding the relationship between events is critical in calculating probabilities accurately.

Probability Calculator by PagesTools.com

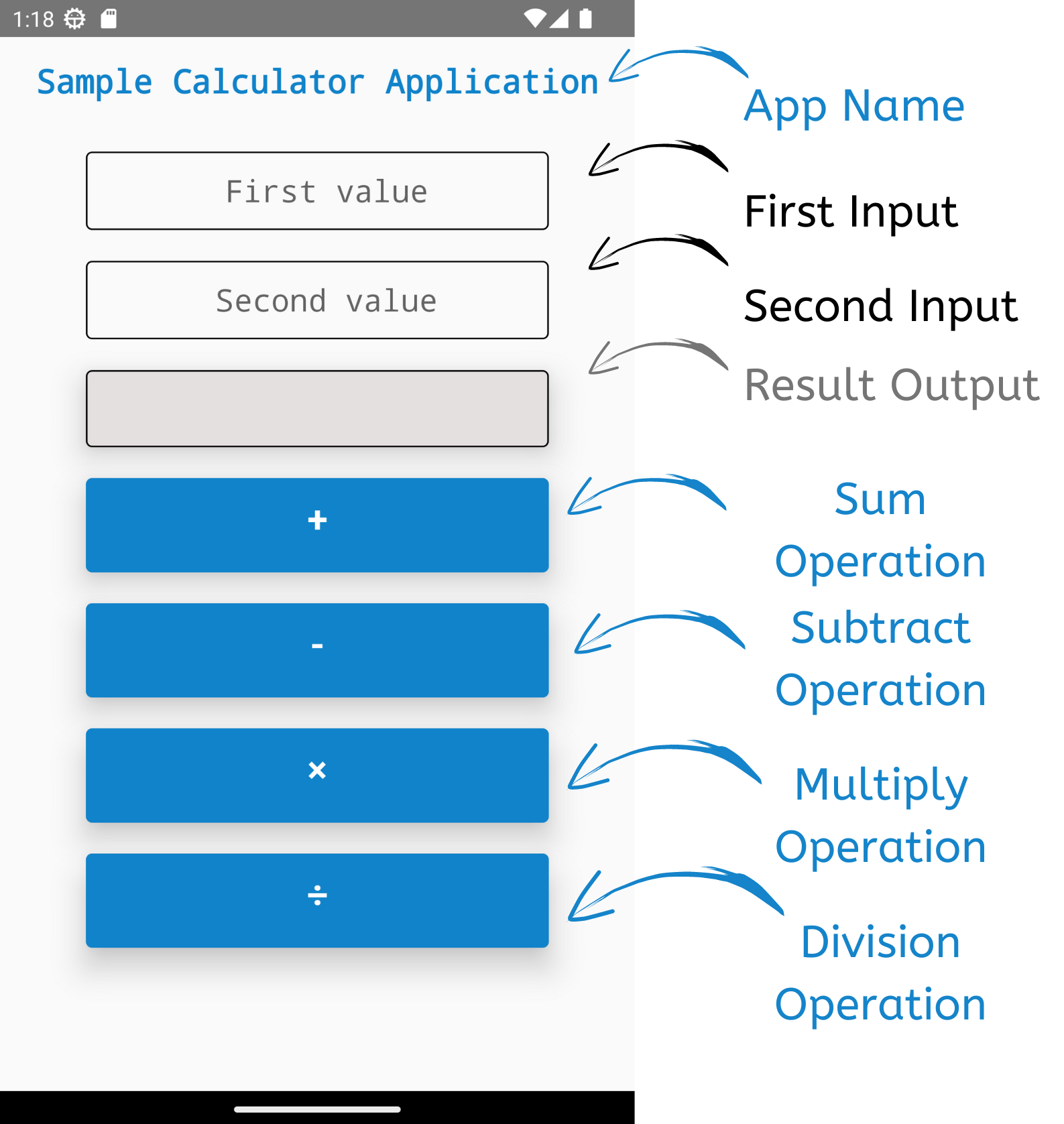
Having established a basic understanding of probability and its types, let’s introduce a tool that makes calculating probabilities simpler - the Probability Calculator by PagesTools.com. It’s designed to help users determine the probability by taking the number of possible outcomes and the number of events that occurred as inputs.

This user-friendly calculator supports computations for both simple and complex probability problems, including probability mass function calculations. By inputting different parameters and probabilities, you can obtain accurate results, making the process of calculating probabilities easier and more efficient.

How to Use a Probability Calculator

Envision possessing a tool that eases the process of calculating probabilities, managing complex calculations, and furnishing the answers you seek. That’s exactly what the Probability Calculator by PagesTools.com does. It’s like having a trusted sidekick ready to assist you in navigating the probability landscape.

Whether you’re dealing with a single event or multiple events, the Probability Calculator has got you covered. To calculate the probability for a single event, you just need to input the number of favorable events observed and the total number of observations. When dealing with more than one event, just move to the next step of the calculator. The calculator utilizes specific formulas tailored to the type of probability and the data provided in order to accurately compute the result. This ensures that the outcome is calculated using the relevant mathematical framework.

Entering Input Values

Initiating with the Probability Calculator is as effortless as providing the input values. For each event, you need to enter the percentage probability in the corresponding fields of the calculator. The calculator adjusts the fields automatically when the number of trials or other input values are changed.

Seems simple, doesn’t it?

Selecting Probability Type

The next step is to select the type of probability calculation. This choice determines which scenarios the calculator will compute. Whether you’re dealing with single events, multiple events or even complex scenarios, the calculator adapts to your needs.

By choosing the correct type of probability calculation, you ensure the accuracy and relevance of the results.

Interpreting Results

And now, the most thrilling part - deciphering the results. Once you’ve entered the input values and selected the probability type, the results are immediately populated on the calculator. It’s like watching a magic trick unfold, where raw odds transform into meaningful probabilities, providing a clear picture of possible outcomes.

Calculating Probabilities for Two Events

What if we have two events instead of one? Does the calculation of probabilities get more intricate? Not if you have the right tools and knowledge! The ‘Probability Solver for Two Events’ is designed to calculate various probabilities involving two independent events. This includes the union and intersection of events, complementary events, and exclusive OR (XOR). You just need to enter the probability of each event, and the calculator will display the probability of six different scenarios:

Both events occurring

Only the first event occurring

Only the second event occurring

Neither event occurring

Either the first or second event occurring (but not both)

Either the first or second event occurring (including both)

Consider the scenario of rolling dice. What’s the probability of getting a specific sum or a certain number on one of the dice? With the Probability Solver for Two Events, you can find the answers to these and other questions, navigating the world of probability with ease and confidence.

Union and Intersection of Events

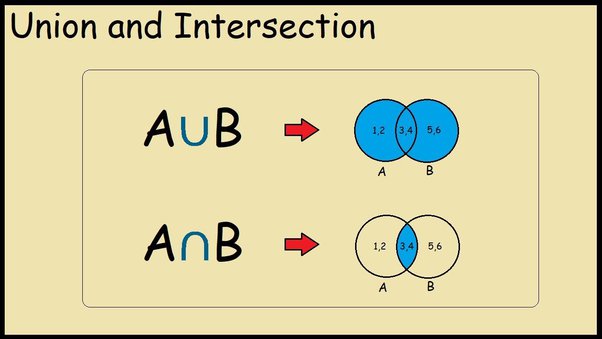
While managing two events, it often becomes essential to determine the union and intersection of the events. The union of two events, denoted as P(A ∪ B), represents the probability that either A or B or both occur. It’s like asking, what’s the chance of drawing a heart or a club from a deck of cards?

On the other hand, the intersection of two events, denoted as P(A ∩ B), represents the probability that both A and B occur simultaneously. Think of rolling two dice and getting a six on both. Understanding these concepts is crucial for calculating probabilities involving two events.

Complementary Events

Complementary events are like two sides of the same coin. They represent two outcomes that cover all possible scenarios. For instance, if you spin a spinner with four colors, the event of landing on red and not landing on red are complementary events.

The probabilities of complementary events always add up to 1. So, if you know the probability of an event, you can easily find its complement by subtracting it from 1.

Exclusive OR (XOR)

Mutually exclusive events are a special type of events where one occurs if and only if the other does not. For example, flipping a coin and getting either heads or tails—these two outcomes are mutually exclusive as both cannot happen at the same time. When calculating probabilities for two events, if the events are mutually exclusive, their joint probability is zero.

This simplifies the union formula to P(A∪B) = P(A) + P(B), giving us a straightforward way to calculate probabilities.

Conditional Probability

Now, let’s delve further into the domain of probability and uncover the concept of conditional probability, which illustrates the interaction between events. Conditional probability is the probability of an event occurring given that another event has already occurred. Think of it as updating your beliefs based on new information.

For example, consider a deck of cards. The probability of drawing an ace is 4/52. But if we know that the drawn card is a heart, the probability changes to 1/13, as there is only one ace in the 13 hearts. This is conditional probability in action, adjusting our expectations based on new information.

Conditional Probability Formula

The formula for conditional probability serves as a mathematical tool to calculate this updated probability, often using the multiplication rule. It’s given by P(A|B) = P(A ∩ B) / P(B), where P(A ∩ B) is the probability of both events A and B occurring and P(A|B) is the probability of A given B has happened.

This formula provides a systematic way to update the probability based on the occurrence of another related event.

Bayes' Theorem

A key tool in understanding and calculating conditional probability is Bayes’ theorem. It’s like a supercharged version of the conditional probability formula, allowing us to reverse conditional probabilities. That is, it can calculate the probability of A given B using the probability of B given A.

This theorem is especially useful in fields such as finance and machine learning for updating predictions with new data.

Probability Distributions

Probability distributions represent another significant concept within probability. They describe the populations of real-life variables, like the height of a group of people or the weight of chicken eggs. These distributions provide a theoretical representation of how often values of a variable occur, giving us a way to model and understand data variability. Some common probability distributions include:

Normal distribution

Binomial distribution

Poisson distribution

Exponential distribution

Uniform distribution

Understanding these distributions is essential for analyzing and interpreting data in various fields, such as statistics, economics, and engineering.

There are two main types of probability distributions: discrete and continuous. Discrete probability distribution describes countable, distinct events, like the number of heads in ten coin tosses, while continuous probability distribution holds information about uncountable events, like the amount of rain in a day.

Discrete Probability Distribution

A discrete probability distribution describes the probability of occurrence of each value of a discrete random variable. A discrete random variable is one that has countable values, like the number of red marbles in a jar or the number of heads when flipping three coins.

The sum of all probabilities in a discrete probability distribution equals one, as it covers all possible outcomes of the variable.

Continuous Probability Distribution

On the other hand, a continuous probability distribution describes the probabilities of possible values of a continuous random variable. A continuous random variable is one that can take an infinite number of values within a range, such as the height of a person or the weight of a bag of sugar. The probability of a continuous random variable assuming a particular value is 0, as there are infinitely many outcomes.

Instead, we talk about the probability of a continuous random variable falling within a certain interval.

Practical Applications of Probability

So far, we’ve delved into the theoretical aspects of probability and investigated its mathematical dimensions. But where does probability find its real-world applications? Well, the answer is—everywhere! Probability plays a pivotal role in various fields, including:

Meteorology

Finance

Sports

Healthcare

A detailed explanation helps experts make informed decisions and accurate predictions.

By understanding probability, it can be applied in various fields:

Insurance companies can assess risks and set premiums for policies.

Coaches and sports analysts use probability to evaluate the performance and strategies of teams and players.

Even in our everyday decisions, like planning a picnic or investing in stocks, understanding the probability can lead to better outcomes.

Probability in Statistics

The field of statistics is where the concept of probability truly stands out. It involves the collection, analysis, interpretation, and presentation of data. And probability is at the heart of all these processes, helping statisticians make sense of complex data and draw meaningful conclusions.

Probability distributions are fundamental in statistics for modeling and understanding data variability. They are often used in hypothesis testing to determine p values and in constructing confidence intervals to express the degree of uncertainty around a parameter estimate. By understanding the statistical applications of probability, we can make more accurate predictions and better decisions.

Probability in Games and Gambling

Games and gambling also assign a unique significance to probability. It’s used to predict outcomes in various games of chance and to calculate expected values—average outcomes of a game if it’s played many times. Understanding probability can give players an edge, helping them make strategic decisions and manage their bets wisely.

For instance, in games like blackjack and poker, understanding the probabilities of different card combinations can improve odds of winning. Similarly, in roulette and dice games, probability can determine the likelihood of specific outcomes, helping players strategize and manage their bets effectively.

Probability in Decision Making

In decision-making, probability serves as a potent tool. Whether it’s a business executive assessing investment risks or a doctor determining the effectiveness of a treatment, understanding probability can lead to more informed and better decisions.

For instance, in finance, probability is used to assess market risks and predict future trends. It’s used in machine learning to make predictions based on past data. Even in everyday decisions, like planning for a picnic or deciding whether to carry an umbrella, understanding probability can help us manage uncertainties and make better decisions.

Theoretical vs Experimental Probability

Now, let’s discuss another crucial facet of probability - the distinction between theoretical and experimental probability. Theoretical probability is based on logical reasoning and known information, while experimental probability is derived from actual experiments and observed outcomes.

While theoretical probability remains constant, experimental probability can vary across different experiments. However, as the number of trials increases, the experimental probability tends to approach the theoretical probability, giving us more accurate results. Understanding these two types of probability can help us grasp the whole picture of probability and its applications.

Theoretical Probability

Theoretical probability is based on mathematical reasoning and known information. It predicts the likelihood of an outcome without experiments, providing a way to estimate probabilities when conducting actual experiments is not feasible.

To calculate theoretical probability, you divide the number of desired outcomes by the total number of possible outcomes. It assumes that all outcomes of a given event are equally likely to occur. For instance, when flipping a coin, the theoretical probability of getting heads is 1/2, as there are two possible outcomes (heads and tails), and each is equally likely.

Experimental Probability

Contrarily, experimental probability, also known as empirical probability, is based on actual experiments and observed outcomes. It gives us a real-world perspective of probability, revealing the actual likelihood of events based on empirical data.

Experimental probability is determined by dividing the number of times an event occurs by the total number of trials conducted. For instance, if a coin is flipped 20 times and lands on heads 14 times, the experimental probability of getting heads is 14/20 or 0.7. It’s a practical, hands-on approach to understanding probability.

Summary

This journey through the world of probability has unveiled the power of this mathematical concept in understanding the world around us and making informed decisions. From defining probability to understanding its types, from learning to use a probability calculator to exploring advanced concepts like conditional probability and probability distributions, we’ve covered a wide range of topics that provide a comprehensive understanding of probability.

Now, you’re equipped with the tools and knowledge to navigate the world of probability, whether it’s calculating odds in a game, assessing risks in business, or making everyday decisions. Remember, understanding probability is not just about crunching numbers—it’s about gaining a deeper understanding of the world and making smart choices.

Frequently Asked Questions

How is probability calculated?

To calculate probability, divide the number of desired outcomes by the total number of possible outcomes.

What is the difference between theoretical and experimental probability?

Theoretical probability is based on logic and known information, while experimental probability comes from actual experiments and observed outcomes. Therefore, the main difference lies in the source of the data and the method of calculation.

What is the role of probability in decision making?

Probability plays a crucial role in decision making by helping to assess risks and predict outcomes, thereby informing decisions in fields such as business, finance, and healthcare.

How is probability used in statistics?

Probability is used in statistics to interpret data and estimate the likelihood of different outcomes, forming the basis of hypothesis testing and constructing confidence intervals. This helps in making informed decisions based on data.

What is the significance of Bayes' theorem in probability?

Bayes' theorem is significant in probability because it allows us to calculate the probability of A given B by using the probability of B given A. This makes it a key tool for calculating conditional probability.